Boolean Identities

This post is about a very basic topic in computer programming, which is boolean logic. The main goal here is to avoid formal notation, just write the Identities in an easy to read format.

(1)

($x || $y) && $z
($x && $z) || ($y && $z) 

(2)

($x && $y) || $z
($x || $z) && ($y || $z)

(3)

$x === $y
!$x XOR $y
$x XOR !$y
true XOR $x XOR $y

(4)

$x XOR $y
!$x === $y
$x === !$y
!($x === $y)

(5)

$x XOR $y
($x + $y) % 2

(6)

($x XOR $y) && $z
($x && $z) XOR ($y && $z)

(7)

($x && $y) || $x
($x || $y) && $x
$x

(8)

$x XOR $x
false

(9)

($x XOR $y) XOR $x
$y

($x XOR $y) XOR $y
$x

(10)

!$x
$x XOR true

(11)

!($x && $y)
!$x || !$y

(12)

!($x || $y)
!$x && !$y

(13)

$x && $y
!(!$x || !$y)
$x XOR $y XOR ($x || $y)

(14)

$x || $y
!(!$x && !$y)
$x XOR $y XOR ($x && $y)

(15)

$x XOR $y
($x || $y) && !($x && $y)
($x && !$y) || (!$x && $y)

(16)

$x && false
false

$x && true
$x XOR false
$x

Median operation

Takes three boolean arguments $x, $y and $z. Evaluates to false if most arguments are false, and true if most arguments are true.

($x && $y) || ($y && $z) || ($x && $z)
($x || $y) && ($y || $z) && ($x || $z)

This is also:

• Monotone Boolean function: it can be expressed in terms of && and ||.
• Self-dual monotone formula: && and || can be interchanged.

For real numbers.

max(min($x, $y), min($y, $z), min($x, $z))
min(max($x, $y), max($y, $z), max($x, $z))

Truth table

Truth table expresses binary function as a binary string. For example, the median operation is 00010111:

f(0,0,0) = 0
f(0,0,1) = 0
f(0,1,0) = 0
f(0,1,1) = 1
f(1,0,0) = 0
f(1,0,1) = 1
f(1,1,0) = 1
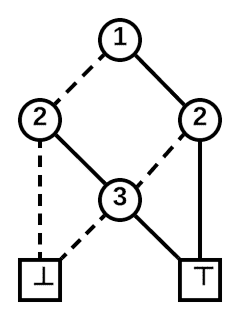
f(1,1,1) = 1

Binary Decision Diagram (BDD)

Binary decision diagram expresses binary function as a diagram. For example, the median operation:

It has the following properties:

• It must be ordered.
• It must be reduced (not waste space).

References

http://www.cs.utsa.edu/~wagner/knuth/ Donald E. Knuth, The Art of Computer Programming Volume 4